[* sudoku.gif >]
Sudoku, zaujímavá to hra na skrátenie dlhej chvíle. Pôvodom z Japonska. Patrí do kategórie logické hry. Dokáže naozaj potrápiť, ale aj zabaviť. Cielom je doplniť chýbajúce číslice podľa daných pravidiel. Tie menšie (menej náročné) sa dajú aj tak povediac z hlavy alebo len pohľadom. Pri tých väčších, zložitejších už treba prísť na systém akým dosiahnuť správneho výsledku, lebo inak nasleduje veľa škrtania, nadávania a trhanie stránok.
Na vlastnej koži som to skúšal, ale poviem vám, radšej si zahrám niečo na mobile alebo budem len tak stáť. Raz som čakal na bus a chlapík si tam vytiahol malinky papierik, ceruzku a poďme: už tam písal, gumoval a prepisoval.
Ja som pre vás našiel rozlúštenie tohto systému, aby ste sa, podobne ako ten pán alebo ja, s tým netrápili.
Na začiatku riešenia sú niektoré políčka vyplnené číslicami. Vyplnené číslice sú rozmiestnené tak, aby pre dané rozmiestnenie existovalo iba jediné riešenie.
Hrací plán sa skladá z 9×9 políčok rozdelených na 9 podoblastí s 3×3 políčkami.
V každej podoblasti sa každá číslica má vyskytnúť práve raz (podoblasti su vyznačené hrubou čiarou).
V každom stĺpci a v každom riadku sa má každá číslica vyskytnúť práve raz.
V princípe možno hrať sudoku aj na plánoch 25×25, 36×36 atď. Aký je rozmer hracieho plánu, toľko potrebujete symbolov.
Pozrieme sa teda koľkými možnými spôsobmi sa dá vyplniť sudoku 4×4 🙂 možno maličké… ale taká chuťovka pred príjazdom autobusu ako vyšitá 🙂
1. krok
Označíme si celkový počet zaplnení ako „C“
Zapíšeme do prvého riadka číslice, nesmú sa opakovať, takže P(4)= 4!
C1=4!
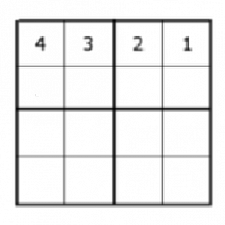
2. krok
Doplníme zostávajúce čísla do štvorčekov
Pre každý štvorček P(2)=2!
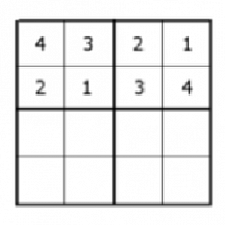
3. krok
Zapíšeme do prvého stĺpčeka 2 čísla.
Na každú pozíciu sa dá zapísať iba jedna z dvoch zostávajúcich čísel.
C3=C2.2!=4!.2!.2!.2!
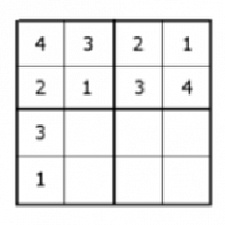
4. krok
Pozícia čísel umiestnených v predchádzajúcom kroku jednoznačne určuje pozíciu týchto čísel v doposiaľ prázdnom štvorci.
5. krok
Tretí a štvrtý stĺpček štvrtého štvorca je tiež daný, po jeho vyplnení sa nám jednoznačne zadájú aj zostavajúce dva riadky. Táto možnosť však nastane iba v určitom naplnení spodného riadka štvorca vpravo hore. Takže počet kombinácií, ktorého výsledok je riešenie tohto sudoku je: C5a=C3a=C2a.2!=(C1.2!).2!=4!.2!.2!=96
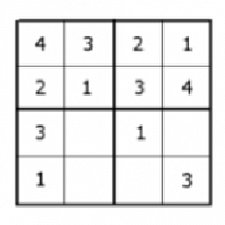
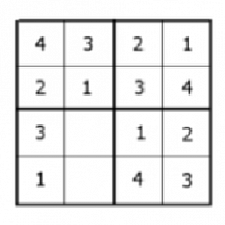
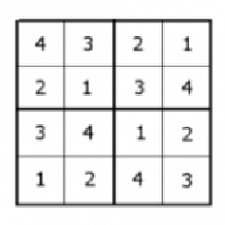
6.krok
Jeden zo stlpcou v štvrtom štvorci je plný. Zaplnením prázdneho štvorca dostávame 2! kombinácii. Táto možnosť však nastane iba vtedy ak sú vyznačené čísla pod sebou. Takže sa vrátime k druhému kroku, kde namiesto dvoch kombinácií zvážime práve tú, ktorá vedie k tomúti prípadu.
C5b=C3b.2!=C2b.2!.2!=(C1.2!).2!.2!=4!.2!.2!.2!
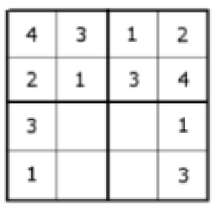
Konečný počet možných riešení je
C=C5a+C5b=192+96=288











